안녕하세요? codingTrip입니다.
오늘은 "코틀린 프로그래밍 1/2(함수편)"
1단원 코틀린의 기본을 익혀요!
2장. 변수와 자료형, 연산자
2-1 기본 자료형과 변수 선언방법 (2) 정수형과 실수형
시작하겠습니다!
🔎 자료형 알아보기
변수의 자료형태에 따라서 담을 수 있는 크기가 정해집니다.
▷ 정수형
- 음수가 사용되는 부호 있는 자료형

Byte는 8비트의 크기를 가집니다. 음수까지 표현하기 때문에 -128부터 127이지만
- 부호 없는 정수형(1.3버전 실험적)

부호가 없는 즉, 음수가 없는 경우에는 0부터 255까지 총 256개의 값을 사용가능합니다.
Byte->Short->Int->Long 순서대로 점점 큰 값이 나오죠?
이걸 토대로 각 값의 크기에 최적화된 자료형을 쓰는 게 좋겠죠.
예를들어, 1부터 10까지의 숫자를 쓴다면 Byte
아주 큰 타입을 다룰 때만 Long을 쓰는 것이 좋습니다.
만약 부호가 없어도 된다면, 부호 없는 정수형을 사용하는 것이 좋겠죠.
그러면 양수쪽에 2배로 더 많은 값을 사용할 수 있습니다.
🧮 자료형 사용의 예
▷ 자료형 생략

첫 번째 줄을 보면 num05라는 이름의 변수에 127라는 값을 넣으면 Int형으로 추론됩니다.
위에 본 표를 참고하여 값의 크기만 보면 Byte형에 들어가지만
기본형으로 자료형이 선언되는 타입은 Int형입니다.
따로 Byte로 표기하지 않는 한 Int형이 추론됩니다.
두 번째, 세 번째 줄까지의 값은 그 크기가 Int형으로 수용가능해서 추론합니다.
그러나 네 번째줄처럼 크기가 너무 큰 값은 Long형으로 추론합니다.
▷ 접미사 접두사 사용

강제로 사용하게 되면 추론형태가 바뀝니다.
예를들어 두 번째 줄 123L처럼 숫자 뒤에 L을 붙이면 Long형으로 추론됩니다.
두 번째 줄처럼 앞에 0x를 붙이면 16진 표기가 사용된 Int형으로 추론됩니다.
16진법은 0에서부터 F까지 사용합니다.
0은 2진법으로 0000 즉, 0을 나타내고,
F는 2진법으로 1111 즉, 16을 나타냅니다.(0에서 시작해서 15입니다.)
0b가 앞에 붙여진 것은 바이너리 표현법입니다.
4자리로 끊어서 보면 좋습니다.
0b/0000/1011으로 나눠서 10진표기법으로 보면
0000->0과 1011->11 즉, 11입니다.
▷ 작은 값의 사용

Byte형으로 선언하고 싶다면 선언 앞쪽에 데이터타입을 기입해야 합니다.
자료형을 지정하지 않고 그냥 넣게되면 Short형 범위라도 Int로 추론합니다.
직접 Short라고 지정해야 합니다.
▷ 부호 없는 정수 자료형
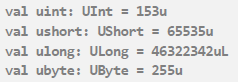
부호가 없는 정수 자료형으로 선언하려면
일단 우리가 맨 앞에 U가 붙어있는 데이터타입으로 선언하고,
맨 뒤에 u를 붙여서 unsigned값이라는 것을 나타내고,
ULong의 경우에는 뒤에 uL로 붙이면 된답니다.
▷ 큰 수를 읽기 쉽게 하는 방법

만약 너무 큰 값이라 읽기 어려우면
_ 언더바를 써서 보기 좋게 구분합니다.
이 기호는 숫자에 어떠한 영향을 미치지 않습니다.
그냥 단순히 우리가 보기 편하게 하는 기호이므로 기호에 맞게 쓰시면 된답니다.
🧪 자료형 알아보기
▷ 실수 자료형

실수형은 Float와 Double이 있습니다.
각각의 크기는 4바이트, 8바이트입니다.
Float 값의 범위는 1.4E-45승 ~ 3.4E+38(IEEE754)라네요.
IEEE754를 선생님께서는 I트리플 E 754라고 읽으시더라고요. (신기)
우리가 실수를 사용할 때 주의할 점이 있어요.
실수는 Double형으로 기본 추론됩니다.
Float을 사용하시려면 Float으로 아예 선언하거나
F를 뒤에 붙여서 Float형으로 추론하게 하면 됩니다.

위의 사진을 토대로 찬찬히 설명해주셨어요.
일반 수학의 표현에서
3.14는 가수이고, 10은 밑수, 그리고 16은 지수라네요.
이걸 소스 코드상의 표현으로 바꾸면
3.14E+16가 된답니다.
3.14처럼 소수점이 있을 수도 없을 수도 있다고 하셨어요.
E는 e혹은 E를 사용가능하답니다.
만약, 이 지수가 음수일 경우에는 +기호에 +대신에 -를 사용합니다.
큰 수(양수)는 왼쪽에서 오른쪽으로 큰 숫자가 되고
작은 수(음수)는 오른쪽에서 왼쪽으로 작은 숫자가 됩니다.
이렇게 소수점을 가지는 실수형으로 표현할 수 있습니다.
만약 여러분이 실수 자료형을 사용할 경우가 생긴다면
여러분이 주의해서 작성해야 한다고 하셨답니다.
🧱 부동 소수점 이해
▷ 32비트와 64비트의 부동 소수점 표현

IEEE 754표준의 float형식
부호, 지수(8비트), 가수(23비트)로 이루어져있습니다.
IEEE 754표준의 double형식
부호, 지수(11비트), 가수(52비트)로 이루어져 있습니다.
딱 봐도 double형식이 더 길다는게 보이시죠?
보시다시피 비트에 제한이 있기 때문에
이것을 넘어서는 숫자는 받아들일 수 없습니다.
▷ -12.375(10)의 표현
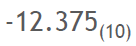
예시를 통해 더 알아볼까요? 10진수로 -12.375인 수에요.
먼저, 음수니까 부호를 - 로 표시했네요.
127이라는 기준값으로 음수를 표현하려고 하고 있습니다.
절댓값인 12.375를 이진수로 표현하려면
1100.011(2)가 나오게 됩니다.
선생님께서는 설명을 안해주셨던 부분이지만
제가 궁금해서 찾아 덧붙이자면
| 2진수 | 10진수 |
| 0.1 | 0.5 |
| 0.01 | 0.25 |
| 0.001 | 0.125 |
| 0.0001 | 0.0625 |
출처 blog.naver.com/undust2/100036033342
즉, 0.375는 0.25+0.125이므로 0.11(2)이 나오게 된거죠.
1100.011(2)에서 소수점을 앞으로 3자리를 빼냅니다.
1.100011*2의 3승이 되겠죠? (10진법이 아니라 2진법이니까요.)
맨 앞 1을 떼어냅니다.
100011을 가수부에 표현하고 나머지는 다 0으로 표현합니다.

2의 3승이니까 기준값인 127에 3을 더해서
10진수로 130을 2진수로 바꾸면 10000010(2)을 지수부에 넣습니다.
꽤 복잡해 보이죠?
1은 -부호 비트로 지정되어서 최종적으로 값을 표현합니다.

👓 IEEE방식의 부동 소수점 제한
▷ 공간 제약에 따른 부동 소수점 연산의 단점

Double 형으로 변수 num을 만들고
for은 반복하는 것이라고 일단 알아두시면 돼요. 자세한 건 나중에 가르쳐주신다고 하셨어요.
0.1을 0부터 999까지 총 1000번을 반복해서 더합니다.
num += 0.1을 풀어 쓰면 num = num+0.1이고요.
아무튼 0.1을 1000번 더하면 된답니다.
원래는 100이 나오게 되겠죠.
근데 소수점 뒤에 값이 이상하게 나왔죠?
바로 공간 제약에 따른 부동 소수점 연산의 단점을 보여주고 있는데요.
정말 코틀린 프로그램에서도 그런지 실습을 통해 확인해볼까요?
💻 예제 실습

새로운 프로젝트를 만들어보겠습니다. Kotlin/JVM을 선택합니다.

프로젝트 이름을 kotlin-part1로 짓습니다.
앞으로는 하나의 프로젝트 안에 모든 걸 생성한다고 하셨어요.

This Window는 현재 윈도우에 새로운 프로젝트를 실행하는 거에요.

기존에는 바로 src폴더에 코틀린 파일을 만들었었죠?
이번에는 폴더를 구분하는 형태를 만들기 위해
Alt+Insert를 한 상태로 Package를 만듭니다.
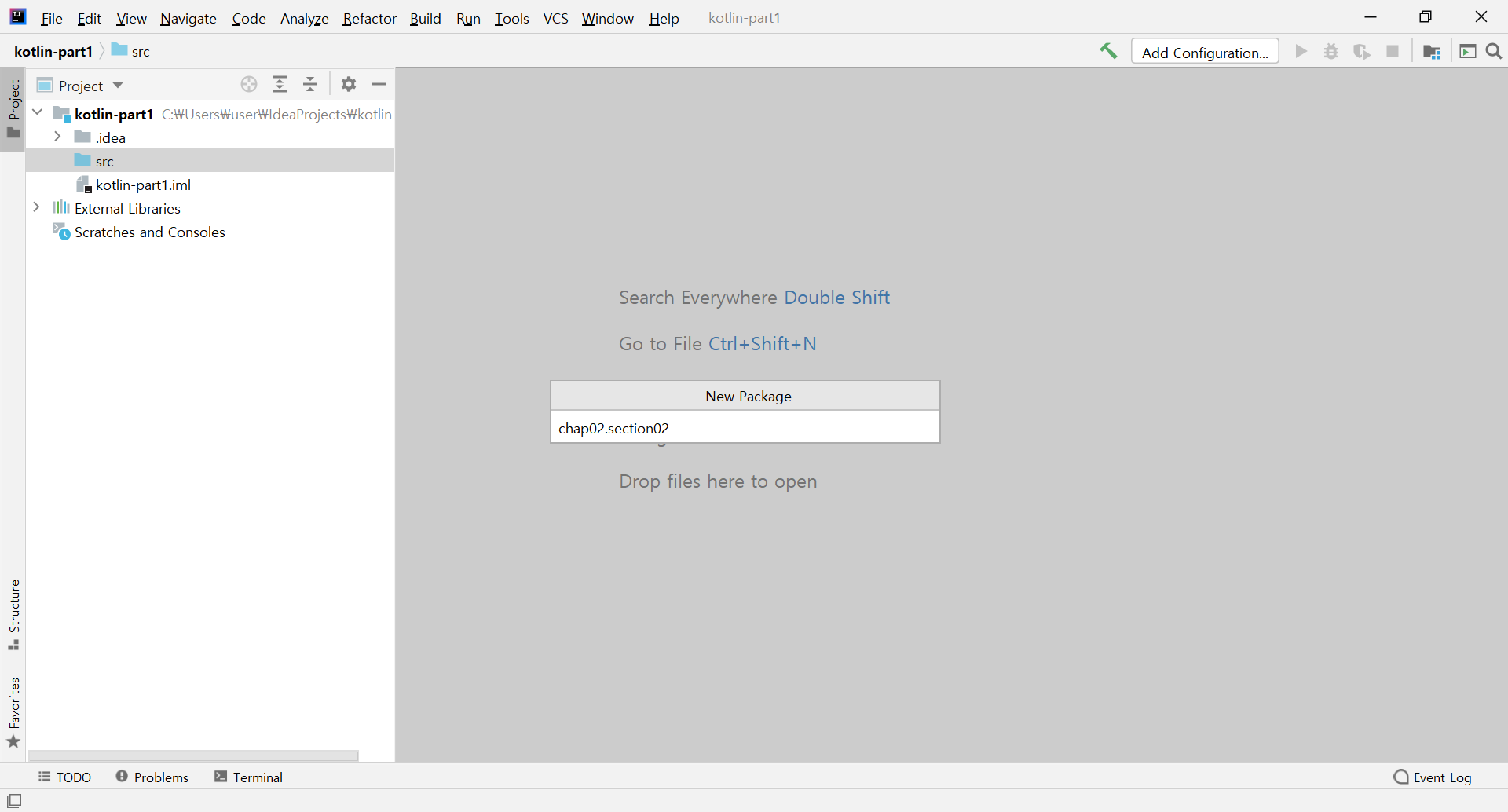
이름은 chap02.section02 이렇게 넣어줍니다.
그러면 보기에는 한 폴더로 보이지만
사실은 폴더 2개로 구분되어 만들어집니다.
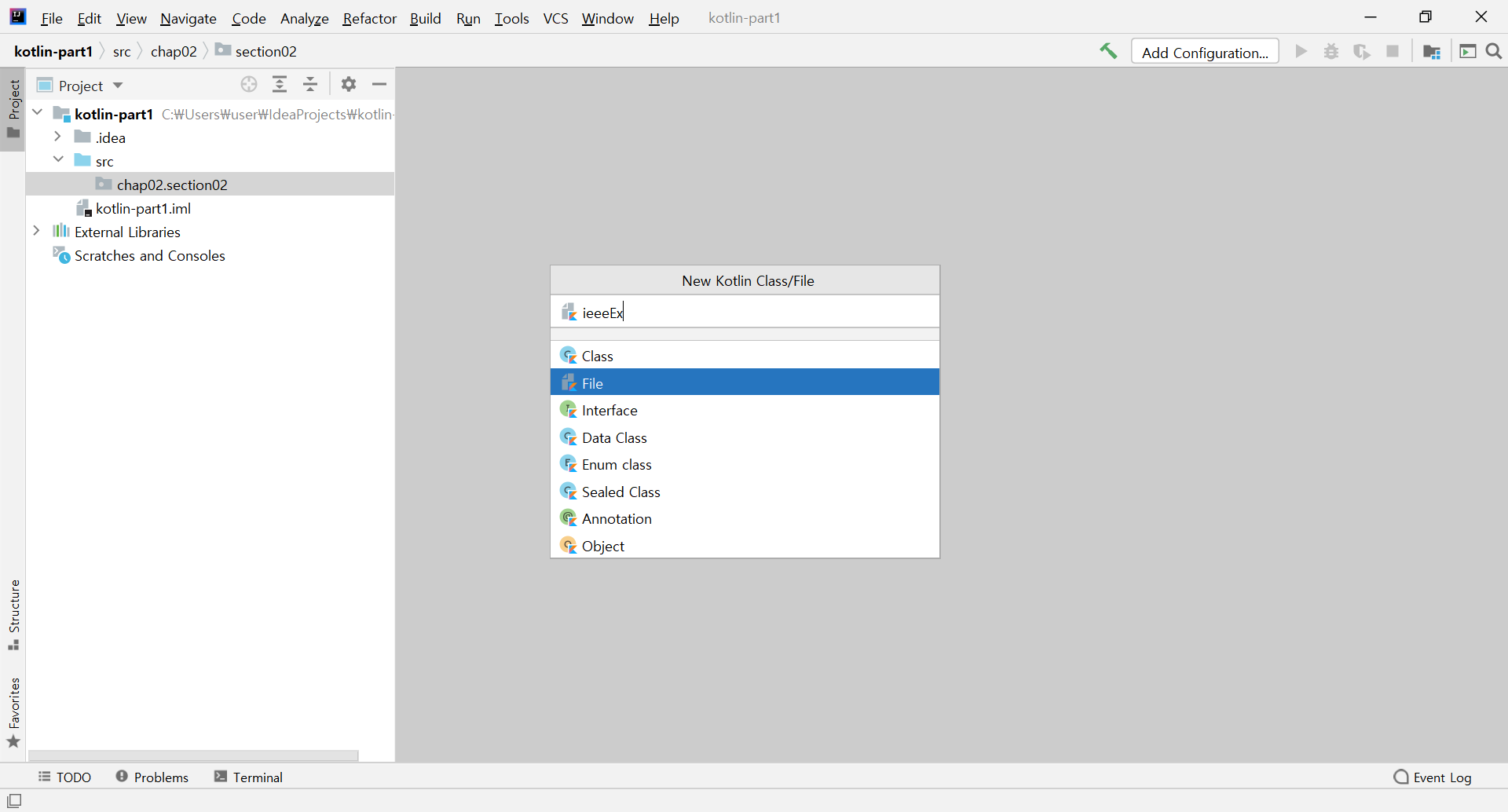
이 chap02.section02폴더를 클릭한채로
Alt+Insert해서 Kotlin File을 만듭니다.
파일 이름은 ieeeEx로 만들어보겠습니다.

패키지를 만들어서 그런지 전에는 없었던 코드가 새롭게 나왔네요.
아래와 같이 코드를 입력합니다.
fun main() {
var num: Double = 0.1
for (x in 0..999){
num += 0.1
}
println("num: $num")
}시작값..끝값 형태로 범위 연산자를 사용할 수 있습니다.
변수 num은 val(불변형)로 하면 할당이 안되니까 var(가변형)로 바꿔줍니다.
결과를 출력하고 실행합니다.
첫 번째 실행은 Alt+Shift+F10 단축키 이제 아시죠? 그리고 2번째를 누르니

결과가 이상하죠? 100이어야 하는데...
지수부와 가수부가 제한이 있기 때문에 이런 현상이 나오는 것입니다.
그러므로 주의를 해야 합니다.
자, 이렇게 이번 시간도 마무리가 되었네요.
코틀린은 일일이 자료형을 설정하지 않아도
기본적으로 코틀린이 알아서 추론할 수 있다는 점이 편한 것 같아요.
선생님께서 실습에서 단축키를 계속 처음처럼 설명해주셔서 좋았어요.
이제 벌써 몇 번째 실습들을 해본거지만
그래도 아직은 손에 안익은 정도로 어색하니까요.
사실 이번 시간에 배운 내용은
처음 알게 되는 개념이 많아서 정말 생소했어요.
3.14E+16? 이게 뭐지? 계산기에서 봤던 것 같아요.
그게 무엇을 뜻하는지는 정확하게 잘 몰랐지만요.
그저 숫자가 많이 커지면 나오는 건가보다 했어요.
0x0F? 0b00001011??
진짜 외계어 같았어요 ㅠㅠ
선생님께서 차근차근 설명해주셨지만
이미 놀란 저의 마음은 쉽게 다독여지지 못했답니다.
이렇게 처음 배워서 생소해서 힘들어하는 사람들을 위해
이 강의는 2개의 강의로 나눠서
더 차근차근 다양한 예시를 보여주시면서
다뤄주셨어도 좋았을 것 같아요.
처음 보는 사람들은 정말 하나도 모르거든요.
내가 이런거를 다 알아야 하나...
나... 코틀린 잘 할 수 있을까...
본격적으로 시작하기도 앞서
여러 가지 고민이 많이 들 수도 있을 것 같아요.
좀 더 초보자에게 눈높이를 맞춰주셨으면 어땠을까하는 아쉬움이 들었습니다.
강의를 다시 촬영하시기 힘드시다면
아래에 더 자세하게 풀어준 자료를 첨부하시는 것을 어떨까요?
우리 너무 벌써부터 겁먹지 말아요.
누가 그랬어요.
어려운게 아니라 처음봐서 어려워보이는 거라고
계속 보다보면 쉬워진다고...
이번 시간에 배운 것도 그럴거에요.
그럼 다음 시간에 또 만나요.

'CODING > 강의노트-부스트코스-코틀린' 카테고리의 다른 글
| [부스트코스]📱코틀린 2-2 나를 괴롭히는 널(Null)! (0) | 2021.01.27 |
|---|---|
| [부스트코스]📱코틀린 2-1 기본 자료형과 변수 선언방법 (3) 크기 범위와 기타 자료형 (0) | 2021.01.22 |
| [부스트코스]📱코틀린 2-1 기본 자료형과 변수 선언방법 (1) 불변형, 기본형 (0) | 2021.01.19 |
| [부스트코스]📱코틀린 1-3 안녕 세상아! (0) | 2021.01.14 |
| [부스트코스] 📱코틀린 1-2 개발 환경을 꾸며 보아요. (2) | 2021.01.12 |